硬核科普系列：用python帮你建立自己的投资组合

作者：码农养基场

听说金融量化很火，当一众金融大佬还在敲打excel的时候，编程技能树早就点满了的程序员是不是开始疯狂抖腿，跃跃欲试。所以小码想开一个硬核科普系列，和大家一起探索如何用python做投资分析。

今天的话题是如何建立投资组合。组成一个投资组合一般都要回答两个问题：1）投资什么 2）每个资产的比例是多少。

可能大部分人可能在主观上可以回答第一个问题，但对于每个资产的投资比例具体是多少，是否有一套可量化的方法在背后呢？小码今天就带大家用python套用经典的马科维兹-均值方差法来计算投资组合比例。

干货预警

warning，这篇文章会有大量干货！！

主要分为三个部分

1、 马科维兹的理论以及均值方差法是什么

2、 让我们用python来尝试一下

3、 理论的局限性

需要花大量时间理解理论部分的童鞋可以先暂且跳过第一部分，直接看第二部分的实操。靴靴！

马科维兹的理论以及均值方差法是什么

哈里马科维茨（Harry M. Markowitz），1927年8月24日生于美国伊利诺伊州。1952年，马科维茨在《金融杂志》上发表题为《资产组合选择——投资的有效分散化》一文，该文堪称现代金融理论史上的里程碑，标志着现代组合投资理论的开端。1990年他也因为这个理论获得诺贝尔经济学奖。
在这篇论文中马科维兹认为，在一定的前提下，可以利用股票的期望收益率和方差找到一条“有效边界”。这条“有效边界”代表着一定预期收益率下风险最小的组合，也代表着相同风险下，收益率最高的组合。
当然，这个理论有几个非常重要的前提和假设：

• 1、投资者都是完全理性，并且厌恶风险的。
• 2、投资者做投资决策只关心两件事：期望收益率和风险。风险体现在证券的波动率，也就是方差上。投资者仅用这两个指标就可以做出投资决策。
• 3、 投资者事先知道投资收益率的概率分布，并且期望收益率满足正态分布的条件。

组合的期望收益率

由于期望收益率满足正态分布，所以整个组合的期望收益率是组合里每个资产的预期收益率的加权平均，权数是每个资产所占的比例。
举个例子：
A股票的期望收益率为10%，B股票为5%。你的组合中A股票占比50%，B股票占比50%，则你的组合的期望收益率是10%*50%+5%*50%=7.5%。

组合的风险

正如假设的那样，组合的风险体现在收益率的波动性上。这里的波动性会有两个组成部分：1）每个资产自身的收益率波动性（收益率的方差） 2）资产之间的联动性风险，即资产之间的协方差。
对于每个资产来说，自身收益率的波动性（收益率的方差）越大，说明实际收益率偏离预期收益率幅度越大，风险就越高。
对于组合中任意两个资产来说（假如都是股票），他们股票价格的变动在一定程度上是有关联性的，因为他们不可避免会受到相同的外部系统风险的影响。
举个例子：沪深300指数下跌幅度很大的时候，通常大部分个股都也随之下跌，尽管下跌的幅度不同。协方差，或者相关系数就是用于判断这种价格变动趋势是否一致。

具体如何计算呢？以2个股票r1、r2组成的组合为例：

股票r的收益波动率：

其中xi是股票的平均收益率，头上戴着帽子的x每天的股票收益率，n是天数

组合的波动率σp 等于：

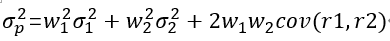
其中，w1是r1的所占比例，σ1是r1的收益率方差，w2是r2的所占比例，σ2是r2的收益率方差，cov(r1,r2)是r1和r2的协方差，也可以简写成σ12。具体的数学推导今天先不展开了~
其实如果放在一个矩阵中会更清晰理解，这是一个2X2的，对角线对称的矩阵。对角线分别是这两个资产的方差，其余的部分是这两个资产的协方差。这个矩阵有个专业名词叫协方差矩阵。

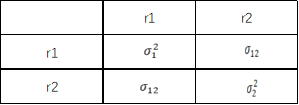
如果是N个股票呢？

同样我们可以用一个NxN的协方差矩阵表示

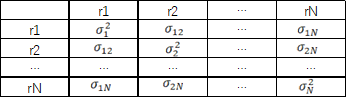
组合的波动率可以表示为：

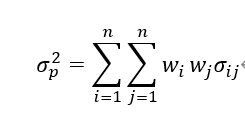
其中i，j表示N个资产中的任意两个资产，wi和wj分别是这两个资产的占比，σij是资产i和资产j的协方差。当i=j的时候，就是指代协方差矩阵中的对角线，也就是各个资产自身的方差。
了解了组合的期望收益率和组合风险的算法之后，你会发现，如果你已经确定了组合里面要投资的资产，组合的期望收益率和风险就仅仅和每个资产的投资比例有关系，因为资产的方差和资产间的协方差在你决定买什么资产的时候也已经确定下来了。
反过来说，如果我可以确定组合的期望收益率，那我是不是可以倒推出资产组合比例和组合的波动率？

让我们用python来尝试一下主要分为5个步骤：

• 1）选择组合里的资产
• 2）计算每个资产每日的收益率 
• 3）计算每个资产的期望收益率和组合的协方差矩阵 
• 4）画出组合的有效边界
•  5) 解读和选择组合比例

第一步：选择组合里的资产

这里推荐大家使用一个免费的财经数据接口包Tushare，可以方便下载和分析金融数据。
这里小码选择了2020/4/3当天沪深300的前10大权重股，并且确保这些股票在2018/4/3至2020/4/3日这段时间内没有异常交易数据。最终小码选择了“民生银行”、“浦发银行”、“上海机场”、“宝钢股份’、’华夏银行’、’华能水电’、’华能国际’、’上港集团’、’浙能电力’、’白云机场’。股价选取的是2018/4/3至2020/4/3的每日收盘价。由于发现“包钢股份”的数据不完整，所以将第11名的“华能水电”代替了“包钢股份”。

%matplotlib inline
import tushare as ts
import pandas as pd
import numpy as np
#选出权重股，可自己调整前xx名
hs300_top10=hs300.sort_values('weight',ascending=False)[:11] #select the first 11 biggst company
name_list=hs300_top10['name']
names=name_list.tolist()
codes=hs300_top10['code'].tolist()

先建立一个空的DataFrame，方便之后数据整合

#获取交易时间段，我这里选择了2018/04/03至2020/04/03两年期间
dates=ts.get_hist_data('hs300',start='2018-04-03',end='2020-04-03').index
stocks=pd.DataFrame(columns=names,index=dates) #set up a empty dataframe

填入每日的股票价格数据

for i in range(0,10):
    data=ts.get_hist_data(codes[i],start="2018-04-03",end="2020-04-03")['close']
    stocks[names[i]]=data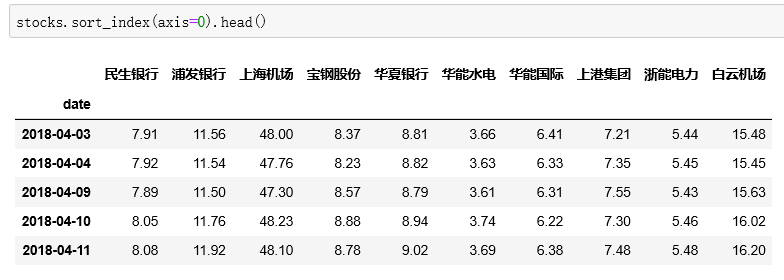

第二步：计算每日的价格变动，即收益率

# Daily percent changes so periods = 1
returns = stocks.pct_change(periods = 1)
returns.dropna(inplace=True)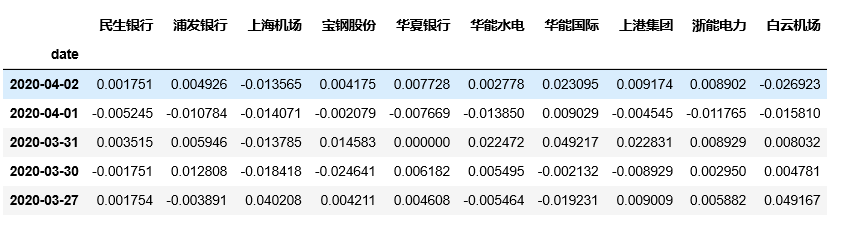

第三步：计算每个资产的期望收益率和协方差矩阵

每个资产的期望收益率是是我预测的未来资产收益率，然而没有人能够准确预测。在实操的过程中，很多时候会用历史的平均值代替未来资产收益率的期望值。所以小码这里也”简单化“处理一下，用过去两年的每日收益率平均值代替每个资产未来的期望收益率（更严谨的操作方式这边先不科普）。

计算每个资产的期望收益率（年化）

assetReturns = returns.mean()#算出每个股票的历史平均收益率
assetCovariance = returns.cov() #算出10个股票之间的协方差矩阵
assetCorrelations = returns.corr() #算出10个股票之间的相关系
numAsset=len(names)
assetReturns * 250 #年化收益率
assetCovariance*252 #年化协方差矩阵

年化收益率

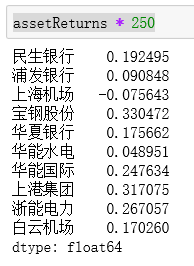
年化协方差

相关系数矩阵

第四步：画出这个组合的有效边界

划重点，有效边界是马科维兹理论中的精华。他认为，有效边界上的投资组合比例才是最优的投资比例。
先定义组合波动率、组合收益率和组合夏普比率的公式。夏普比率代表投资人每多承担一分风险，可以拿到几分超额报酬。假如夏普比率是2，说明投资者每承担1份的风险，可以收获2份的超额收益。

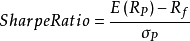
其中E(Rp)：投资组合预期报酬率
Rf：无风险利率，例如国债收益率，是你不需要担心任何风险就能得到的投资回报率σp：投资组合超额收益的标准差（即方差的算数平方根）

def portfolioVariance(weights): #计算组合方差
    weights = np.array(weights)
    var = np.dot(weights.T, np.dot(assetCovariance * 252, weights))
    return var

def portfolioVolatility(weights): #计算组合标准差
    return np.sqrt(np.dot(weights.T, np.dot(assetCovariance * 252, weights)))

def portfolioReturn(weights): #计算组合的收益率
    return np.sum(assetReturns * weights) * 252

def portfolioSharpeRatio(weights): #计算组合夏普比率
    return (portfolioReturn(weights) - rfr) / portfolioVolatility(weights)

先定义一些需要的参数

rfr = 0.015 #无风险利率，这里可变
portfolioReturns = []
portfolioVolatilies = []

导入SciPy.Optimize优化函数

import scipy.optimize as sco

利用scipy.optimize，我们可以算出不同的组合期望收益率对应的组合波动率、每个资产的比例和夏普比率。我这里设定了一个限制：所有资产比例总和加起来要等于1，也就是说要求电脑算法100%利用所有的股票。

minRet = min(assetReturns*252)
maxRet = max(assetReturns*252)
trets = np.linspace(minRet, maxRet, 50)
tvols = []
weights=[]
sharpe=[]
initialWeights = np.ones(numAsset)
bnds = tuple((0, 1) for x in initialWeights)

for tret in trets:
    cons = ({'type': 'eq', 'fun': lambda x:  portfolioReturn(x) - tret},
            {'type': 'eq', 'fun': lambda x:  np.sum(x) - 1})

    res = sco.minimize(portfolioVolatility, initialWeights, method='SLSQP', bounds=bnds, constraints=cons)
    frontierWeights = res['x']
    frontierRet = portfolioReturn(frontierWeights)
    frontierVol = portfolioVolatility(frontierWeights)    
    tvols.append(res['fun'])
    weights.append(frontierWeights)
    sharpe.append((frontierRet-rfr)/frontierVol)

以组合期望收益率为y轴，组合波动率为x轴，画出有效边界

import matplotlib.pyplot as plt
plt.figure(figsize=(16, 8))
plt.scatter(tvols, trets, c=(trets-rfr) / tvols, marker='o')
plt.grid(True)
plt.xlabel('Expected volatility')
plt.ylabel('Expected return')
plt.colorbar(label='Sharpe ratio')

第五步：解读和选择组合比例

上图中每个点，代表是一种投资比例得到的组合期望收益率（y轴）和组合波动率（x轴），右边的彩条显示的是夏普比率。
夏普比率越高，说明同等风险下获得的收益率越高。在上面的图中可以看到有效边界上的组合夏普比率普遍高于0.8，而无效边界的夏普比率普遍低于0.8.
无效边界之所以是无效的，是因为在同等或者相似的风险下（波动率），可以找到更好的投资组合比例，使得组合收益率更高。你可以尝试垂直x轴画一条线，这条垂线会和整条边界线有两个交点，一个在上面的有效边界上，一个在下面的无效边界上。有效边界上的交点代表的投资组合有更高的收益率，而且它的风险和无效边界上的组合是差不多的。所以，对于理性的投资者，有效边界上的组合才是值得投资的。根据在这个逻辑，我们还能发现一个风险最小的组合，这个组合被马科维兹称为Global Minimum Variance Portfolio——全球最小方差组合，它为于整条边界线的最左端。

红框部分便是GMV组合对应的投资比例

可以筛选出夏普比率大于0.9的的投资组合

Sharpe_Ratio=pd.DataFrame(sharpe,columns=["Sharpe Ratio"])
find_highest_ratio=Sharpe_Ratio[Sharpe_Ratio["Sharpe Ratio"]>=0.9].index
Weights=pd.DataFrame(weights,columns=names)
Weights.loc[find_highest_ratio]

夏普比率大于0.9的的投资组合比例

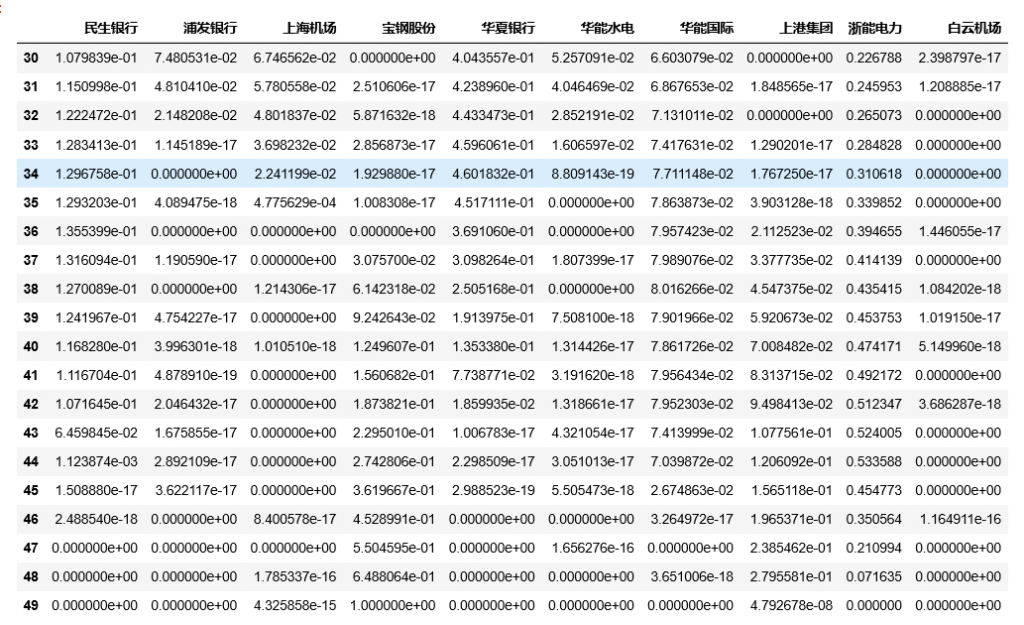
可以发现，随着夏普比率越来越高，组合的集中度也越高，集中在收益率高的个股上。而集中度高的组合，风险分散能力较低，组合的波动性也会比较大。所以，这是一个你需要权衡风险和收益率的决定。

理论的局限性

20世纪50年代，马科维兹这个理论可谓是革命性的创新。因为他首次应用资产组合报酬的均值和方差这两个数学概念，从数学上明确地定义了投资者偏好。第一次将边际分析原理运用于资产组合的分析研究。但是这个理论也有局限性：
1、 现实的投资者并不是完全理性的；2、 期望收益率以及波动率的预测有非常高的误差，模型的参数稍有调整，输出的结果就有比较大的变动。比如，如果我不是用近两年的股价数据，而是用近三年的数据，那么有效边界的形状会有较大的变化；而且预测未来的收益率和波动率难度非常大3、 股价在现实生活中并不是正态分布的。
因此马科维兹的均值-方差法可以你决作为定组合比例的参考，但实际做投资决策的时候一定要谨慎哦。